基于概率论的分类方法：朴素贝叶斯

本章内容
使用概率分布进行分类
学习朴素贝叶斯分类器
解析RSS源数据
使用朴素贝叶斯来分析不同地区的态度

朴素贝叶斯算法(Naive bayes)是有监督的学习算法，解决的是分类问题，如客户是否流失、是否值得投资、信用等级评定等多分类问题。该算法的优点在于简单易懂、学习效率高、在某些领域的分类问题中能够与决策树、神经网络相媲美。但由于该算法以自变量之间的独立（条件特征独立）性和连续变量的正态性假设为前提，就会导致算法精度在某种程度上受影响。本文主要讲解如何在实际环境中应用朴素贝叶斯算法，同时涉及如何使用Python工具和相关机器学习术语，算法原理详见朴素贝叶斯分类器 详细解析。

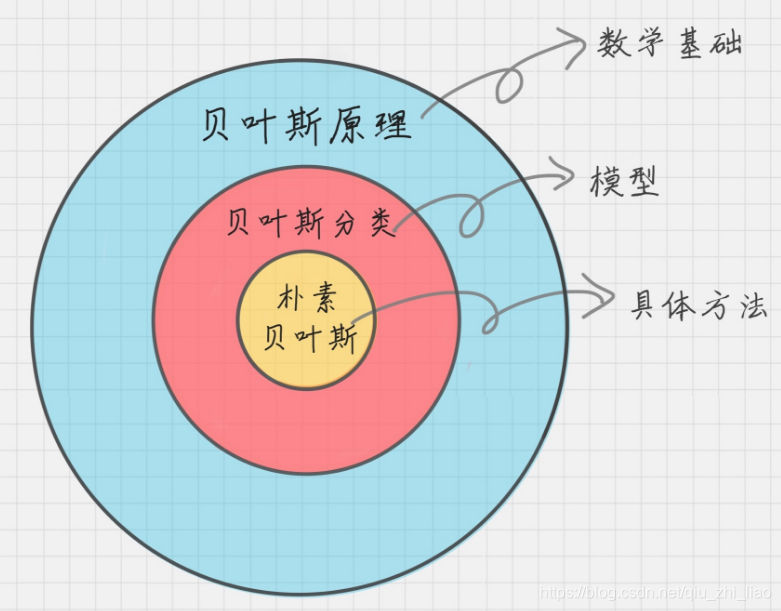
基于贝叶斯决策理论的分类方法

朴素贝叶斯

优点：在数据较少的情况下仍有效，可以处理多类别问题。
缺点：对于输入数据的准备方式较为敏感。
适用数据类型：标称型数据。

朴素贝叶斯是贝叶斯决策理论的一部分，假设现在我们有一个数据集，它由两类数据组成，数据分布如下图所示：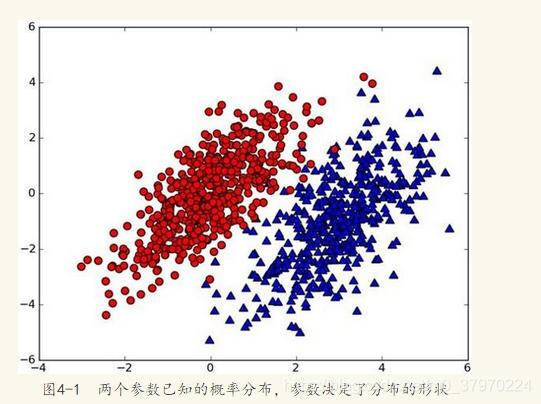

我们现在用p1(x,y)表示数据点(x,y)属于类别1(图中红色圆点表示的类别)的概率，用p2(x,y)表示数据点(x,y)属于类别2(图中蓝色三角形表示的类别)的概率，那么对于一个新数据点(x,y)，可以用下面的规则来判断它的类别：

· 如果p1(x,y) > p2(x,y)，那么类别为1
· 如果p1(x,y) < p2(x,y)，那么类别为2

也就是说，我们会选择高概率对应的类别。这就是贝叶斯决策理论的核心思想，即选择具有最高概率的决策。

使用朴素贝叶斯进行文档分类

机器学习的一个重要应用就是文档的自动分类。在文档分类中，整个文档(如一电子邮件)是实例，而电子邮件中的某些元素则构成特征。
朴素贝叶斯是贝叶斯分类器的一个扩展，是用于文档分类的常用算法。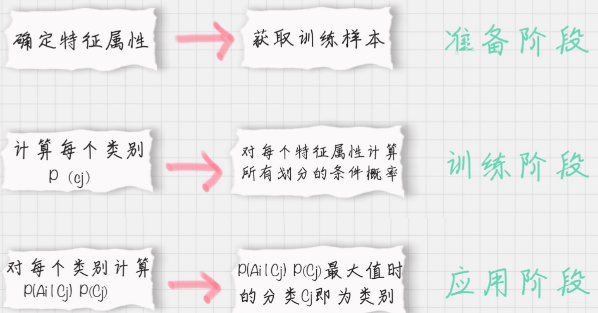

朴素贝叶斯的一般过程

(1) 收集数据：可以使用任何方法。本文使用RSS源。
(2) 准备数据：需要数值型或者布尔型。
(3) 分析数据：有大量特征时，绘制特征作用不大，此时使用直方图效果更好。
(4) 训练算法：计算不同独立特征的条件概率。
(5) 测试算法：计算错误率。
(6) 使用算法：可以在任意的分类场景中使用朴素贝叶斯分类器。

使用Python进行文本分类

要从文本中获得特征，需要先拆分文本。这里的特征是来自文本的词条(token)，一个词条是字符的任意组合。可以把词条想象为单词，也可以使用非单词词条，如URL、IP地址或者任意其他其它字符串。然后将每一个文本片段表示为一个人词条向量，其中值为1表示词条出现在文档中，0表示词条未出现。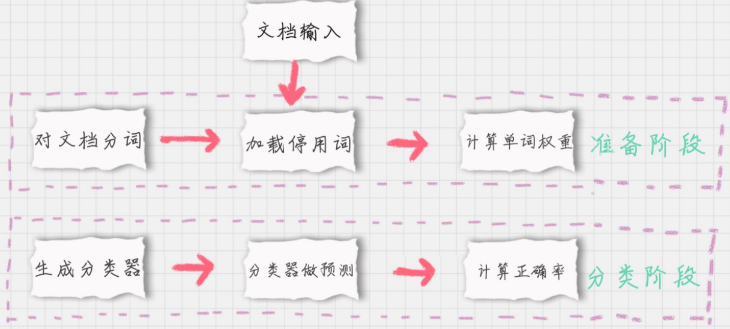

准备数据：从文本中构建词向量

我们把文本看成单词向量或者词条向量，也就是说将句子转换为向量。考虑出现所有文档中的单词，再决定将哪些单词纳入词汇表或者说所要的词汇集合，然后必须要将每一篇文档转换为词汇表上的向量。简单起见，我们先假设已经将本文切分完毕，存放到列表中，并对词汇向量进行分类标注。
词表到向量的转换函数

def loadDataSet():
    postingList=[['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],
                 ['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
                 ['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
                 ['stop', 'posting', 'stupid', 'worthless', 'garbage'],
                 ['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
                 ['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
    # 1 is abusive, 0 not
    classVec = [0,1,0,1,0,1]
    return postingList,classVec
                 
def createVocabList(dataSet):
    # create empty set
    vocabSet = set([])
    for document in dataSet:
        # union of the two sets
        vocabSet = vocabSet | set(document)
    return list(vocabSet)

def setOfWords2Vec(vocabList, inputSet):
    returnVec = [0]*len(vocabList)
    for word in inputSet:
        if word in vocabList:
            returnVec[vocabList.index(word)] = 1
        else: print("the word: %s is not in my Vocabulary!" % word)
    return returnVec

函数loadDataSet()创建了一些实验样本，该函数返回的第一个变量是进行词条切分后的文档集合。loadDataSet()返回的第二个变量是一个类别标签的集合。这里有两类，侮辱性和非侮辱性。
函数createVocabList()会创建一个包含在所有文档中出现的不重复词的列表，为此使用了Python的set数据类型。
获得词汇表后，便可以使用函数setOfWords2Vec()，该函数的输入参数为词汇表及某个文档，输出的是文档向量，向量的每一个元素为0或1，分别表示词汇表中的单词在输入文档中是否出现。

训练算法：从词向量计算概率

我们已经得到了词条向量。接下来，我们就可以通过词条向量训练朴素贝叶斯分类器，该函数的伪代码如下：

计算每个类别中的文档数目
对每篇训练文档：
　　对每个类别：
　　　　如果词条出现在文档中->增加该词条的计数值
　　　　增加所有词条的计数值
对每个类别：
　　对每个词条：
　　　　将该词条的数目除以总词条数目得到条件概率
返回每个类别的条件概率

该函数的Python实现使用了NumPy的一些函数，所以首添加from numoy import *。
朴素贝叶斯分类器训练函数

from numpy import *

def trainNB0(trainMatrix,trainCategory):
    numTrainDocs = len(trainMatrix)
    numWords = len(trainMatrix[0])
    pAbusive = sum(trainCategory)/float(numTrainDocs)
    p0Num = zeros(numWords); p1Num = zeros(numWords)
    p0Denom = 0.0; p1Denom = 0.0
    for i in range(numTrainDocs):
        if trainCategory[i] == 1:
            p1Num += trainMatrix[i]
            p1Denom += sum(trainMatrix[i])
        else:
            p0Num += trainMatrix[i]
            p0Denom += sum(trainMatrix[i])
    p1Vect = p1Num/p1Denom
    p0Vect = p0Num/p0Denom
    return p0Vect,p1Vect,pAbusive

代码函数中的输入参数为文档矩阵trainMatrix，以及由每篇文档类别标签所构成的向量trainCategory。函数的返回值为两个向量一个概率，p0Vect以及p1Vect代表在给定文档类别条件下词汇表中单词的出现概率(条件概率)，pAbusive代表任意文档属于侮辱性文档的概率。

测试算法：根据现实情况修改分类器

运用trainNB0()函数进行分类之前，还需要解决函数中的一些缺陷。

问题1： 利用贝叶斯分类器对文档进行分类时，要计算多个概率的乘积以获得文档属于某个类别的概率，即计算p(w0|1)p(w1|1)p(w2|1)。如果其中有一个概率值为0，那么最后的成绩也为0；
解决： 所有词的出现数初始化为1，并将分母初始化为2。这种做法就叫做拉普拉斯平滑(Laplace Smoothing)又被称为加1平滑，是比较常用的平滑方法，它就是为了解决0概率问题。
问题2： 下溢出，由于太多很小的数相乘，计算结果可能就变成0了，
解决： 对乘积结果取自然对数。通过求对数可以避免下溢出或者浮点数舍入导致的错误。

问题1的解决办法称为拉普拉斯平滑(Laplacian smoothing)，是解决零概率的问题的常用方法。
问题2的解决办法采用了取对数法，ln(f(x))会随f(x)的增大而增大，这表明想求函数的最大值时，可以使用该函数的自然对数来替换原函数进行求解。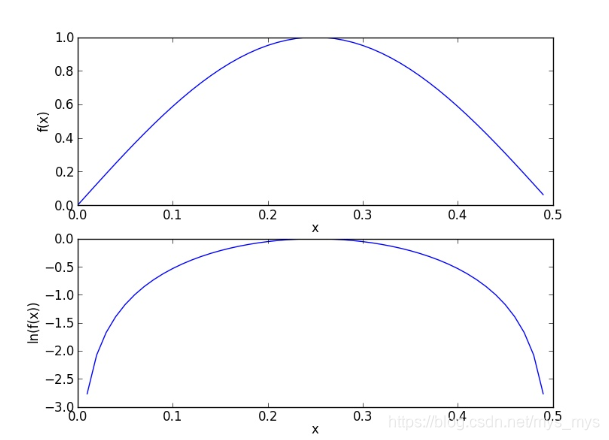

现在使用NumPy向量处理功能构建完整的分类器。
朴素贝叶斯分类函数

def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1):
    # element-wise mult
    p1 = sum(vec2Classify * p1Vec) + log(pClass1)
    p0 = sum(vec2Classify * p0Vec) + log(1.0 - pClass1)
    if p1 > p0:
        return 1
    else: 
        return 0

def testingNB():
    listOPosts,listClasses = loadDataSet()
    myVocabList = createVocabList(listOPosts)
    trainMat=[]
    for postinDoc in listOPosts:
        trainMat.append(setOfWords2Vec(myVocabList, postinDoc))
    p0V,p1V,pAb = trainNB0(array(trainMat),array(listClasses))
    testEntry = ['love', 'my', 'dalmation']
    thisDoc = array(setOfWords2Vec(myVocabList, testEntry))
    print(testEntry,'classified as: ',classifyNB(thisDoc,p0V,p1V,pAb))
    testEntry = ['stupid', 'garbage']
    thisDoc = array(setOfWords2Vec(myVocabList, testEntry))
    print(testEntry,'classified as: ',classifyNB(thisDoc,p0V,p1V,pAb))

分类函数需要4个输入：要分类的向量vec2Classify以及使用函数trainNB0()计算得到的三个概率。最后比较类别的概率返回大概率对应的类别标签。

准备数据：文档词袋模型

词集模型(set-of-words model)： 将每个词的出现与否作为特征，即将出现单词的对应数值设为1。
词袋模型(bag-of-words model)： 将每个词出现的次数作为特征，即将出现单词的对应数值增加1。

def bagOfWords2VecMN(vocabList, inputSet):
    returnVec = [0]*len(vocabList)
    for word in inputSet:
        if word in vocabList:
            returnVec[vocabList.index(word)] += 1
    return returnVec

示例：使用朴素贝叶斯过滤垃圾邮件

示例：使用朴素贝叶斯对电子邮件进行分类

(1) 收集数据：提供文本文件。
(2) 准备数据：将文本文件解析成词条向量。
(3) 分析数据：检查词条确保解析的正确性。
(4) 训练算法：使用trainNB0()函数。
(5) 使用classifyNB()，并且构建一个新的测试函数来计算文档集的错误率。
(6) 构建一个完整的程序对一组文档进行分类，将错分的文档输出到屏幕上。

测试算法：使用朴素贝叶斯进行交叉验证

我们将文本解析器和分类器集成到一个完整的函数当中，函数将读取数据集email文件夹下的spam和ham数据，并对其进行交叉验证。
文件解析及完整的垃圾邮件测试函数

#input is big string, #output is word list
def textParse(bigString):
    import re
    listOfTokens = re.split(r'\W*', bigString)
    return [tok.lower() for tok in listOfTokens if len(tok) > 2] 
    
def spamTest():
    docList=[]; classList = []; fullText =[]
    for i in range(1,26):
        wordList = textParse(open('email/spam/%d.txt' % i).read())
        docList.append(wordList)
        fullText.extend(wordList)
        classList.append(1)
        wordList = textParse(open('email/ham/%d.txt' % i).read())
        docList.append(wordList)
        fullText.extend(wordList)
        classList.append(0)
    # create vocabulary
    vocabList = createVocabList(docList)
    # create test set
    trainingSet = range(50); testSet=[]
    for i in range(10):
        randIndex = int(random.uniform(0,len(trainingSet)))
        testSet.append(trainingSet[randIndex])
        del(trainingSet[randIndex])  
    trainMat=[]; trainClasses = []
    # train the classifier (get probs) trainNB0
    for docIndex in trainingSet:
        trainMat.append(bagOfWords2VecMN(vocabList, docList[docIndex]))
        trainClasses.append(classList[docIndex])
    p0V,p1V,pSpam = trainNB0(array(trainMat),array(trainClasses))
    errorCount = 0
    # classify the remaining items
    for docIndex in testSet:
        wordVector = bagOfWords2VecMN(vocabList, docList[docIndex])
        if classifyNB(array(wordVector),p0V,p1V,pSpam) != classList[docIndex]:
            errorCount += 1
            print("classification error",docList[docIndex])
    print('the error rate is: ',float(errorCount)/len(testSet))
    #return vocabList,fullText

第一个函数textParse()接受一个大写字符串并将其解析为字符串。该函数去掉少于两个字符的字符串，并将所有字符串转换为小写。
第二个函数spamTest()对贝叶斯垃圾邮件分类器进行自动化处理。导入spam和ham文件夹下的数据并构建一个训练集和测试集。遍历测试集，对其中每封邮件进行分类，最后给出总的错误百分比。

总结

1.在训练朴素贝叶斯分类器之前，要处理好训练集，文本的清洗还是有很多需要学习的东西。
2.根据提取的分类特征将文本向量化，然后训练朴素贝叶斯分类器。
3.去高频词汇数量的不同，对结果也是有影响的的。
4.拉普拉斯平滑对于改善朴素贝叶斯分类器的分类效果有着积极的作用。

---

🤯本文作者：Ivan
🔗本文链接：
🔁版权声明：本站所有文章除特别声明外，均采用©BY-NC-SA许可协议。转载请注明出处！